Definitions for quadratic polynomial
qua·drat·ic po·ly·no·mi·al

Princeton's WordNetRate this definition:0.0 / 0 votes

1. quadratic, quadratic polynomialnoun

   a polynomial of the second degree

WikipediaRate this definition:0.0 / 0 votes

1. quadratic polynomial

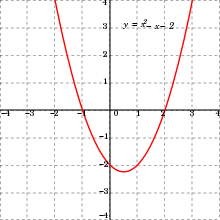
   In mathematics, a quadratic polynomial is a polynomial of degree two in one or more variables. A quadratic function is the polynomial function defined by a quadratic polynomial. Before 20th century, the distinction was unclear between a polynomial and its associated polynomial function; so "quadratic polynomial" and "quadratic function" were almost synonymous. This is still the case in many elementary courses, where both terms are often abbreviated as "quadratic". For example, a univariate (single-variable) quadratic function has the form f ( x ) = a x 2 + b x + c , a ≠ 0 , {\displaystyle f(x)=ax^{2}+bx+c,\quad a\neq 0,} where x is its variable. The graph of a univariate quadratic function is a parabola, a curve that has an axis of symmetry parallel to the y-axis. If a quadratic function is equated with zero, then the result is a quadratic equation. The solutions of a quadratic equation are the zeros of the corresponding quadratic function. The bivariate case in terms of variables x and y has the form f ( x , y ) = a x 2 + b x y + c y 2 + d x + e y + f , {\displaystyle f(x,y)=ax^{2}+bxy+cy^{2}+dx+ey+f,} with at least one of a, b, c not equal to zero. The zeros of this quadratic function is, in general (that is, if a certain expression of the coefficients is not equal to zero), a conic section (a circle or other ellipse, a parabola, or a hyperbola).

ChatGPTRate this definition:0.0 / 0 votes

1. quadratic polynomial

   A quadratic polynomial is a polynomial of the second degree, which can be represented by the general formula ax^2+bx+c where a, b, and c are constants, a ≠ 0, and x is a variable. It produces a graph in the shape of a parabola when plotted on a graph.

WikidataRate this definition:3.8 / 4 votes

1. Quadratic polynomial

   In mathematics, a quadratic polynomial or quadratic is a polynomial of degree two, also called second-order polynomial. That means the exponents of the polynomial's variables are no larger than 2. For example, is a quadratic polynomial, while is not.

Matched Categories

1. • Polynomial

How to pronounce quadratic polynomial?

1. Alex

   US English

   David

   US English

   Mark

   US English

   Daniel

   British

   Libby

   British

   Mia

   British

   Karen

   Australian

   Hayley

   Australian

   Natasha

   Australian

   Veena

   Indian

   Priya

   Indian

   Neerja

   Indian

   Zira

   US English

   Oliver

   British

   Wendy

   British

   Fred

   US English

   Tessa

   South African

How to say quadratic polynomial in sign language?

Numerology

1. Chaldean Numerology

   The numerical value of quadratic polynomial in Chaldean Numerology is: 9

2. Pythagorean Numerology

   The numerical value of quadratic polynomial in Pythagorean Numerology is: 1

References

1. ^ Princeton's WordNet
   http://wordnetweb.princeton.edu/perl/webwn?s=quadratic polynomial
2. ^ Wikipedia
   https://en.wikipedia.org/wiki/Quadratic_Polynomial
3. ^ ChatGPT
   https://chat.openai.com
4. ^ Wikidata
   https://www.wikidata.org/w/index.php?search=quadratic polynomial